Last updated on 2024. 11. 24.
도블이라는 보드게임에 숨겨진 수학 원리를 제 나름대로 공부한 결과를 정리했습니다.
1. 들어가기
어떤 보드게임을 했는데 대략적인 게임 방식은 다음과 같습니다. 총 7명의 캐릭터가 있는데 주사위를 굴려서 나온 눈 만큼 캐릭터 하나를 골라 움직일 수 있습니다. 다른 사람도 같은 방식으로 진행하고 모든 캐릭터를 선택해서 움직일 수 있습니다. 캐릭터 색깔은 무지개 색깔로 빨강, 주황, 노랑, 초록, 파랑, 남색, 보라 이렇게 있습니다. 카드를 잘 섞어서 한 장 나눠주는데, 거기에 3명의 색깔 캐릭터가 그려져 있습니다. 이제 나의 미션은 이 3명을 최대한 많이 이동시키는 것입니다. 내가 어떤 캐릭터인지 숨기고 몰래 캐릭터를 전진시켜야 하는 게임입니다.
그런데 다른 사람도 카드를 한 장 받을 것이고 거기에도 3명의 색깔 캐릭터가 그려져 있겠죠. 또 다른 사람도 마찬가지… 그런데 총 7인까지 할 수 있으니깐 7장의 카드가 있습니다. 여기서 중요한 점은 카드를 어떻게 분배하더라도 서로 겹치는 색깔의 캐릭터가 반드시 한 색깔이 있고, 나머지 두 색깔은 겹치지 않는다는 점입니다. (반 협력이 될지도?)
저의 의문의 시작점이 바로 여기입니다. 어떻게 하면 카드를 이렇게 만들 수 있을까요? 그리고 곧 이것이 도블이라는 보드게임과 원리가 똑같다는 것을 알게 되었습니다. 총 7장의 카드에 3가지 색깔이 그려져 있고 서로 다른 카드 두 장을 비교하면 반드시 같은 색깔이 1개 있는 것이죠. 미니 도블인 셈입니다. 일단 이것에 대한 답을 만들어 보면 다음과 같습니다.
2. 기본예제
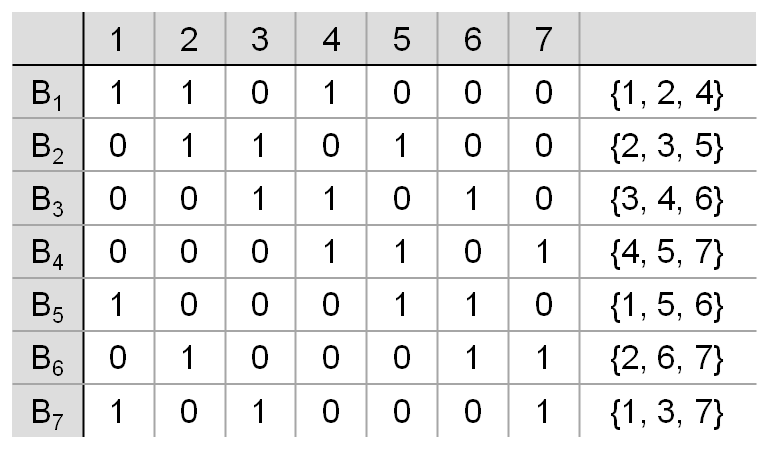
(7, 3, 1) 예제
여기서 1, 2, 3, 4, 5, 6, 7 이 각각 빨, 주, 노, 초, 파, 남, 보 이렇게 생각하면 됩니다. 즉 7종류(v)가 있습니다. 카드 장수 7장(b)이 필요합니다. 그것을 B1, B2, …. , B7으로 표현하였습니다. 카드마다 3개의 색깔(k)이 그려져 있습니다. 이제 임의의 카드 두 장을 뽑아 서로 비교해 봅시다. 예를 들어 B2 카드(주, 노, 파)와 B6 카드(주, 남, 보)를 비교해 보면 서로 주황색만 공통으로 들어 있습니다. 임의의 두 장의 카드를 가져오더라도 이런 식으로 딱 한 색깔만 겹쳐 있습니다. 이러한 블록 디자인에 대한 개인적으로 스터디 한 내용을 적어보려고 합니다.
용어에 대한 정의를 내리고 수식으로 정리하기 위해 논의를 더 이어가겠습니다. 비슷한 내용처럼 보이는데 이번에는 관점을 카드(행)가 아닌 색깔(열)로 봅시다. 서로 다른 임의의 두 개의 색깔을 골라봅시다. 여기선 3번-노란색 열과 5번-파란색 열을 골라서 비교하면 해당 색깔이 공통으로 나오는 카드는 B2; 1개(λ) 입니다. 그리고 3번-노란색이 나오는 카드는 B2, B3, B7 이렇게 총 3번(r) 나옵니다. 반복 횟수라고 적어볼게요.
조금 어려운 용어라서 정확한 정의보다는 개념적으로 대강 적어 보면 7종류 색깔을 그보다 적은 3개씩 몇 개의 블록으로 쪼개서 (여기서는 총 7장의 카드를 사용했으니 7블록으로 나누어서) 각 색깔이 동일한 반복 횟수만큼 나오면서도 서로 다른 두 개의 색깔을 골랐을 때 1개의 블록에서만 고른 색깔이 공통으로 나오는 이러한 블록 디자인을 Balanced Incomplete Block Design 이라고 정의합시다. 앞으로 줄여서 BIBD 라고 적겠습니다. (숫자는 좀 변경될 수 있고 정확한 정의가 아닐 수도 있지만 내용이 너무 딱딱해 지는 것을 방지하고자 함이니 이해를 부탁)
3. 추가예제
위에서 정의한 (v, k, λ)의 의미를 짚어보기 위해 몇 가지 예제를 만들었습니다.
(v, k, λ)=(6, 3, 2) 예제
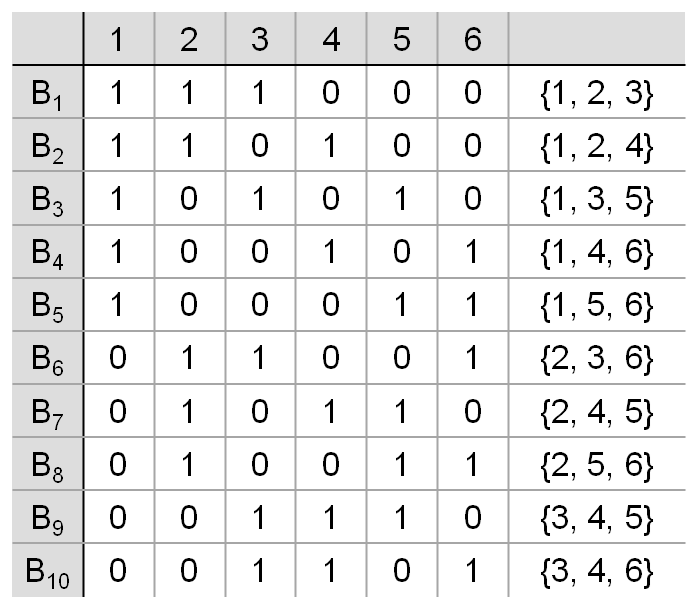
(6, 3, 2) 예제
6종류(v)의 색깔이 있고 이 중 3가지(k) 색깔을 골라 10장의 카드를 만드는 디자인 중에서 서로 다른 두 개의 색깔이 2개(λ)의 블록에서만 같이 나오도록 하는 디자인입니다. 여기서 λ의 의미 파악이 쉽지 않을 수도 있어서 그림을 추가했습니다.
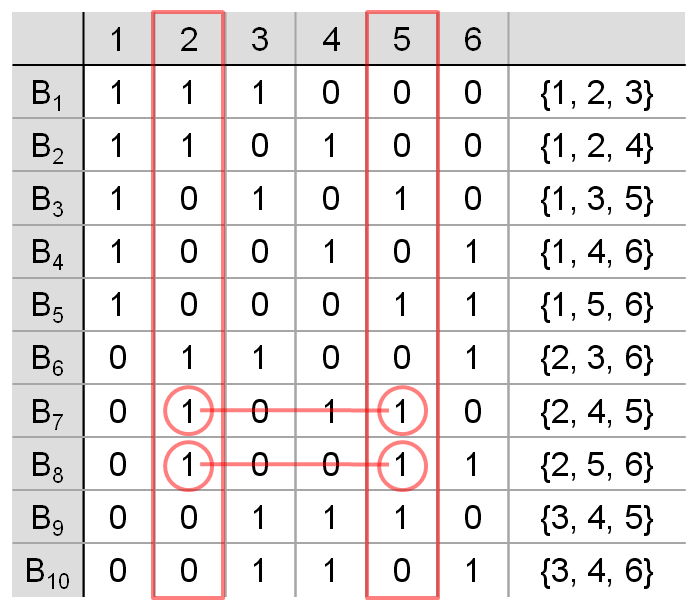
(6,3,2) 예제 보충설명1
서로 다른 두 개의 색깔; 예를 들어 2번과 5번 색깔을 골라봅시다. 그러면 해당 색깔이 같이 나오는 블록은 B7과 B8 이렇게 2개(λ)입니다. 이것이 λ에 대한 정의입니다. 반복횟수를 보면 2, 5번 색깔은 총 5번씩(r) 사용됩니다. 또 다른 예제를 들어봅시다.
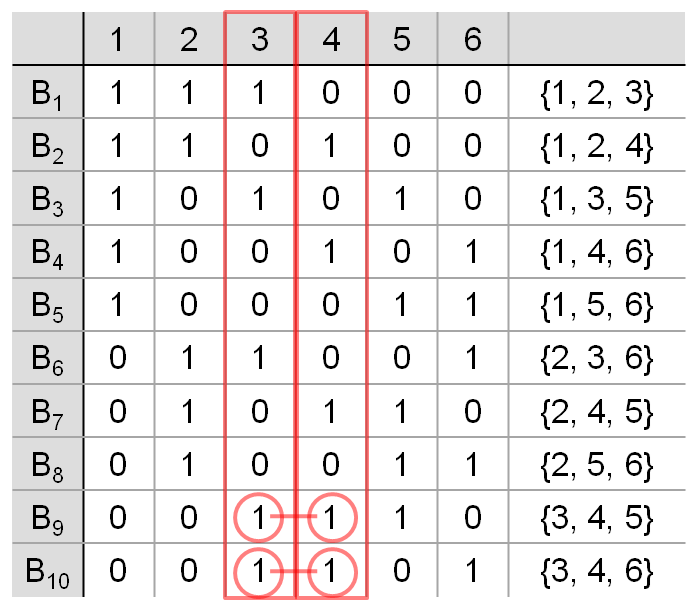
(6, 3, 2) 예제 보충설명2
이번에는 서로 다른 두 개의 색깔; 예를 들어 3번과 4번 색깔을 골라봅시다. 그러면 해당 색깔이 같이 나오는 블록은 B9과 B10 이렇게 2개(λ)입니다. 마찬가지로 반복횟수는 3, 4번 색깔도 총 5번씩(r) 사용됩니다. 이것뿐만 아니라 임의의 서로 다른 두 개의 색깔을 고르더라도 마찬가지입니다. 이제 λ의 정의는 어느 정도 이해되었을 것이라 봅니다. 그러면 이제 용어를 정의해봅시다.
4. 용어정의 및 수식
b: 블록의 수 v: 종류의 개수 k: 각각 블록안의 종류의 개수 r: 한 종류가 총 몇 번 반복되는지 즉 반복 횟수를 나타냄. \lambda: 서로 다른 두 종류를 골랐을 때, 몇 개의 블록에서 선택한 두 종류가 같이 나오는지를 나타냄.Theorem. BIBD(v, k, λ)에서 다음 식이 성립합니다.
\lambda(v-1)=(k-1)r … (4.1)
bk=vr … (4.2)
증명) 아래 그림을 보면서 이해해 봅시다. 용어를 그림으로 나타낸 것입니다.
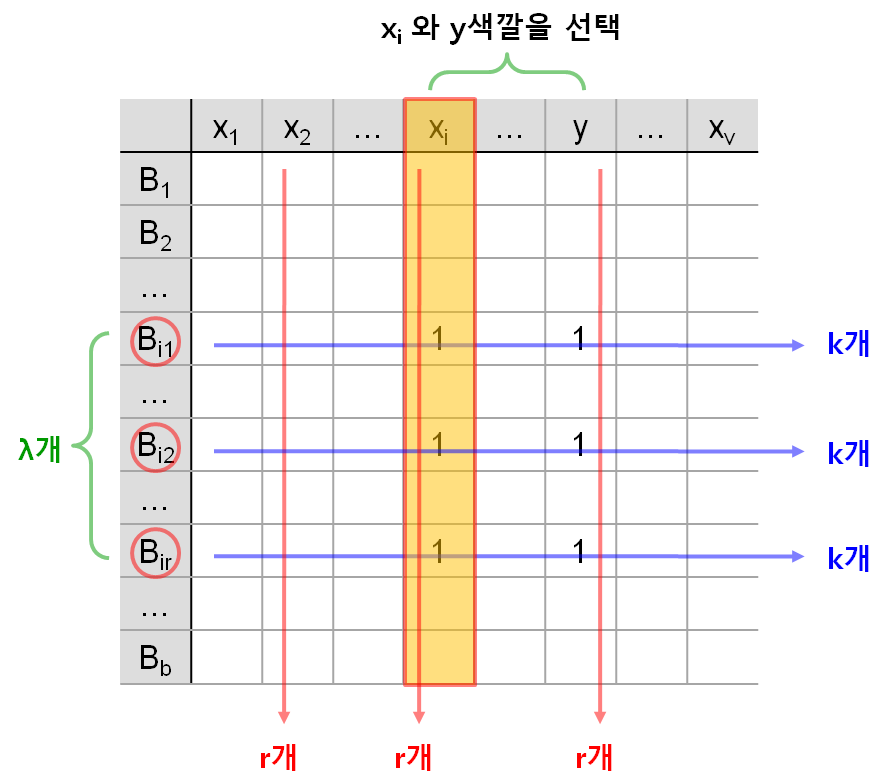
(4.1) 수식 증명
우리의 목표는 x_i 를 제외한 열(주황색 음영을 제외한) 나머지 숫자의 합계를 구하는 게 목표입니다. 두 종류의 색깔 x_i 와 y 를 선택합니다. 그러면 λ개 블록에서 선택한 색깔이 나옵니다. 이러한 y를 몇 개나 고를 수 있을까요? x_i 자신을 제외하고 선택할 수 있으므로 총 (v-1)개 입니다. 그러면 총 개수는
\lambda(v-1).
이 됩니다.
한편, x_i 열을 제외하면 각 블록당 가로 개수는 k-1개 이고 각 색깔은 반복 횟수가 r번씩 이므로
(k-1)r.
가 됩니다. 서로 다른방법으로 카운드 한 숫자가 서로 같으므로
\lambda(v-1)=(k-1)r.
이 되어 (4.1) 증명이 끝납니다. (4.2)는 위와 비슷하게 전체 숫자를 카운트하는 방식으로 따져보면 이해가 될 거라 생각되네요. (4.1), (4.2)를 통해 다음을 유도할 수 있습니다.
b=\dfrac{v(v-1)}{k(k-1)}
v, k, λ의 값이 설계되면 b와 r 값을 구할 수 있고 여기서 모든 값은 정수라는 것을 기억해 둡시다.
5. 예제 더 알아보기
(1) (v, k, λ)=(9, 3, 1) 예제
b=\dfrac{9*8}{3*2}=12 블록이 필요함을 알 수 있습니다.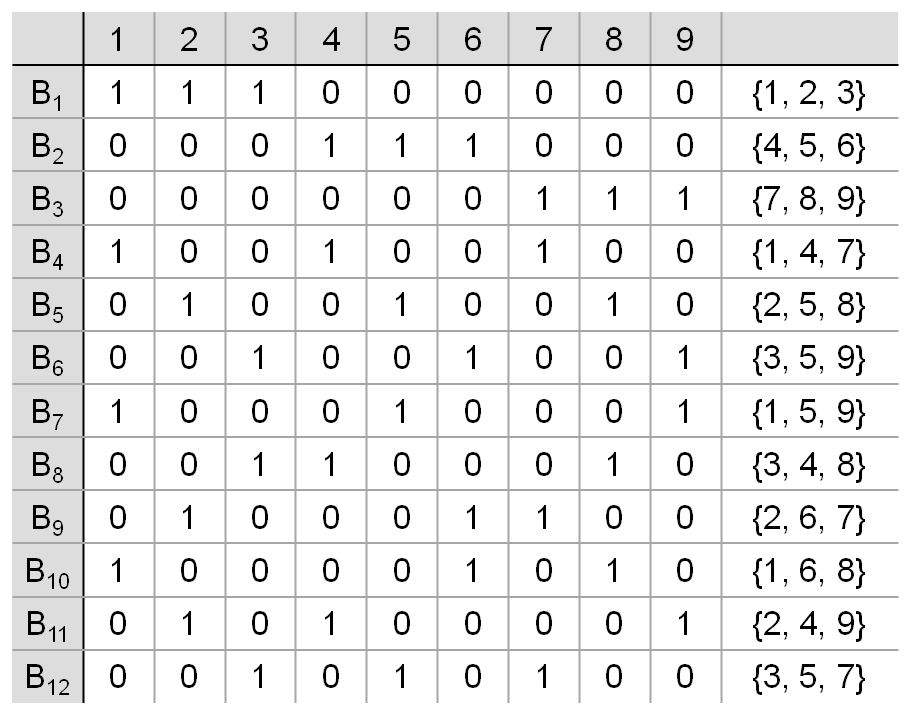
(9, 3, 1) 예제
서로 다른 두 개의 색깔; 예를 들어 2번과 6번 색깔을 골라봅시다. 그러면 해당 색깔이 같이 나오는 블록은 B9; 1개(λ)뿐 입니다.
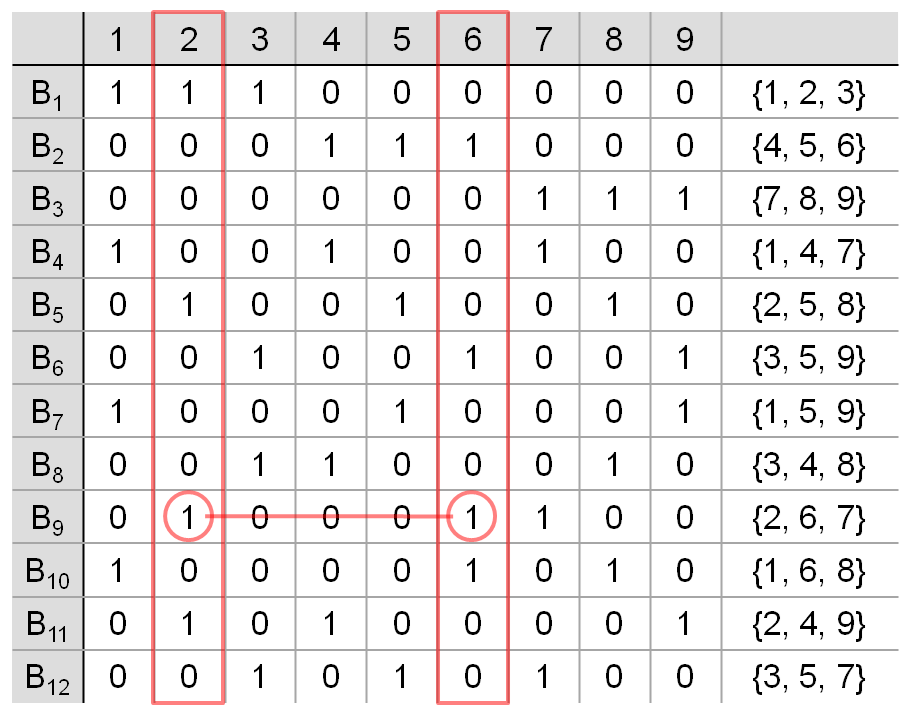
(9, 3, 1) 예제 보충설명
비교적 유명한? 예제 위주로 가져왔는데 그러면 어떤 (v, k, λ)를 가져오더라도 BIBD를 만들 수 있는지 궁금해졌습니다.
아래는 안되는 예제인데 비슷하게 만들어 봤습니다.
(2) (v, k, λ)=(6, 3, 1) 예제
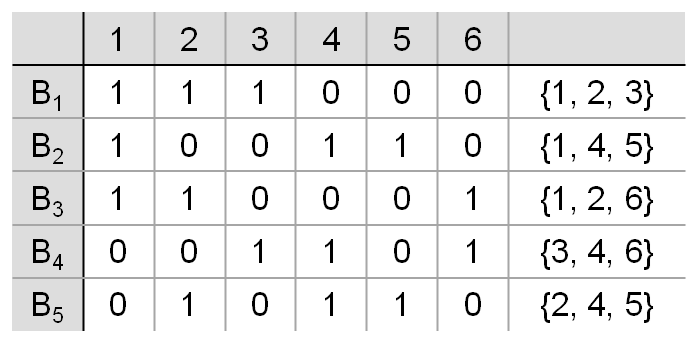
(6, 3, 1) 안되는 예제
그럴듯하게 비슷하게 만들었습니다. 2번 색깔을 기준으로 다른 색깔과 비교했습니다.
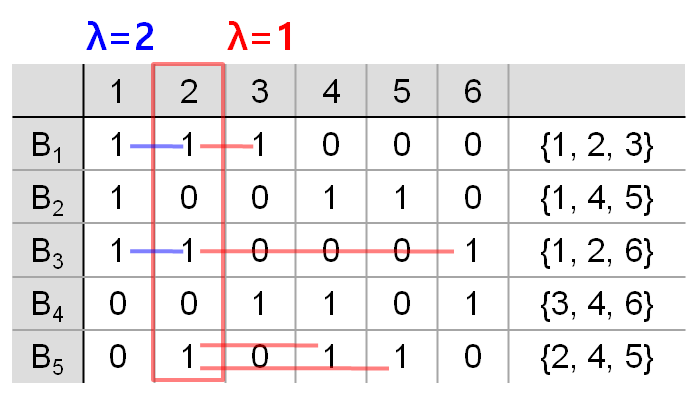
(6, 3, 1) 예제 보충설명
2-3 색깔을 선택하면 B1에서; 2-4 색깔을 선택하면 B5에서; 2-5 색깔을 선택하면 B5에서; 2-6 색깔을 선택하면 B3에서만 선택한 색깔이 나오므로 λ=1로 잘 된 거 처럼 보일 수 있습니다. 하지만, 2-1 색깔을 비교하면 B1, B3 이렇게 두 군데에서 선택한 색깔이 나오므로 이쪽은 λ=2로 되었습니다. 실제로 위에 수식 (4.1)에 (v, k, λ)=(6, 3, 1)을 넣어보면 r=5/2 가 나와서 정수가 안됩니다. 그러므로 BIBD 설계가 안 됩니다. 사실 반복 횟수 r도 색깔마다 다릅니다.
다음 내용을 간단히 체크하고 넘어갑시다. (증명은 조금 복잡하므로 여기선 생략)
Theorem. BIBD라면, b\ge v.
즉, 종류의 개수보다 블록 수가 같거나 많아야 합니다.
6. 그래서 도블이랑 어떻게 연결되나요?
위의 복잡한 변수들을 조정해서 특별한 케이스를 만들어 봅시다. 특별히 블록개수=종류개수 즉, b=v가 되는 경우를 생각해 봅시다. 지금까지 위의 테이블에서 가로는 v를 표현했고 세로는 b를 표현했으니 행과열의 길이가 같아지겠죠. 여기에 λ=1 인 경우만 생각합시다. 행과열의 길이가 같아졌으므로 이제 λ=1 을 블록(카드)간 겹치는 색깔이 한 개라는 친숙한(?) 의미로 해석할 수 있겠습니다.
b=v 이므로 수식(4.2)에서 자동적으로 k=r 이 되고 이걸 (4.1)에 넣고 정리해보면
v=k(k-1)+1 … (6.1)
이 됩니다.
이게 뭔 뜻이냐면 맨 처음으로 돌아가서 k의 의미를 살펴보면 전체 종류에서 카드에 그려지는 종류의 수를 의미하죠. 첫 보드게임에서는 카드 한 장당 서로 다른 3개의 색깔 캐릭터가 그려져 있었죠. k=3 입니다. 이것을 (6.1)에 대입하면 v=7 이 나옵니다. 즉, 7종류의 색깔이 있으면 7장의 카드를 준비해서 서로 다른 3가지 색깔 캐릭터를 잘 그려놓으면 λ=1 카드간 겹치는 색깔이 한 개만 나오도록 설계가 가능하게 됩니다.
도블은 카드 한 장당 서로 다른 8개의 캐릭터가 그려져 있었죠. k=8 입니다. 이것을 (6.1)에 대입하면 v=57 이 나옵니다. 즉, 57종류가 있고 57장의 카드를 준비해서 서로 다른 8가지 캐릭터를 잘 그려놓으면 λ=1 카드간 겹치는 캐릭터가 한 개만 나오도록 설계가 가능하게 됩니다.
그런데 도블카드는 2장을 빼놓은 55장만 있다고 합니다. 2장을 빼놓은 이유를 찾아보니 몇 가지 있던데 저의 뇌피셜은 큰 종이 원단 한 장에 11장씩 나와서 뭔가 비용적인 문제가 있지 않았겠느냐는 상상을 해봅니다. 촘촘히 배치하려면 4/3/4로 제작하지 않았을까…?
그냥 추측입니다;
7. 좀 더 생각해 볼거리
(1) 위에 예제에서 k=3, 8인 경우를 다뤘는데 그러면 k=4, 5, 6, 7인 경우는 어떨까요? 그러면 각각 v=13, 21, 31, 43 값이 나오니깐 BIBD 를 만들 수 있겠죠. 특별히 (v, k, λ)=(43, 7, 1)을 생각해 봅시다. 43종류의 캐릭터를 준비하고 43장의 카드를 준비해서 서로 다른 7가지 캐릭터를 그리는 경우겠죠.
그런데 이 경우는 BIBD를 만들 수 없다고 합니다. 수식을 계산해도 모든 값들이 정수값으로 나와도 말이죠. 즉, 모든 값들이 정수인 것은 BIBD의 필요조건이지 충분조건이 되지 않습니다. 이게 또 유명한 36명의 장교 배치 문제 – 직교 Latin Square 문제와 연관이 있는 거 같습니다.
(2) (v, k, λ)=(13, 4, 1)은 BIBD를 만들 수 있을까요?
가능합니다. ChatGPT에 물어보니 금방 만들어 주네요. 행렬 형태로 표현하면 보기 쉬우나 양이 너무 많은 거 같아서 밑에 집합으로 표현했습니다. 그것보다 의문점은 아래 방법이 유일한 것인가? 몇 개나 만들 수 있을까? 어떻게 만드는 방법이 있을까? 였는데 아직 거기까진 공부하진 못했네요. 다음에 더 공부하게 되면 따로 적어보렵니다.
답: {1 2 3 4}, {1 5 6 7}, {1 8 9 10}, {1 11 12 13},
{2 5 8 11}, {2 6 9 12}, {2 7 10 13},
{3 5 9 13}, {3 6 10 11}, {3 7 8 12},
{4 5 10 12}, {4 6 8 13}, {4 7 9 11}
이걸로 13장 짜리 미니도블이 가능하겠네요.
(3) Projective planes 중에 특별한 Case로 Fano plane이 있습니다. 사실 맨 처음에 나온 (v, k, λ)=(7, 3, 1)과 동일한 것인데 인터넷 검색으로 많이 나오는 거 같으니 한번 찾아보셔요.
❑ References
- https://en.wikipedia.org/wiki/Block_design: Block design
- Richard A. Brualdi. (1999). Introductory combinatorics (3rd ed.), Prentice-Hall, ISBN 0-13-181488-5
